字符串匹配

RuyiWei...大约 12 分钟

字符串匹配

一、KMP算法

模式串与主串做匹配时，如果是暴力匹配，在主串某趟匹配失败后，模式串要移动第一位，而主串也有苦难需要回退。

在KMP算法中，如果在匹配过程中，主串不需要回退，当匹配失败后，会从当前位置开始继续匹配。而模式串会滑动到某一位开始比较，而不是没都回退到第一位开始比较。

1、前缀表

前缀：除最后一个字符以外，字符串的所有头部子串。
后缀：除第一个字符以外，字符串的所有尾部子串。

需要找的是每个子串前缀和后缀相等的最长的前缀和后缀的长度。

求前缀表

以 abcac 为例：

子串	前缀	后缀	最长相等前后缀长度
a	-	-	0
ab	a	b	0
abc	ab、a	bc、c	0
abca	abc、ab、a	bca、ca、a	1
abcac	abca、abc、ab、a	bcba、cac、ac、c	0

下标	0	1	2	3	4
字符串	a	b	c	a	c
前缀表 prefix	0	0	0	1	0

所以，字符串 abcac 的最长相等前后端长度是 00010，将这个长度写成数组形式，得到

对应的部分匹配值 [0,0,0,1,0] ，换成另一个名字是，前缀表 prefix = [0,0,0,1,0]

模拟匹配过程

下面，将模式串 abcac 与主串 ababcabcacbab 进行匹配

第一趟：

主串指针 len = 2 ，模式串指针 i = 2 时，模式串的 c 和主串的 a 匹配失败。已经匹配的字符串是 ab ，查看前缀表，prefix[1] = 0 ，说明 ab 前缀和后缀没有相等的，所以下一趟模式串要回退到第一个字符重新比较，也就是回退到模式串 pattern 的下标为 0 的位置。

下标	0	1	2	3	4	5	6	7	8	9	10	11	12
主串 main	a	b	a	b	c	a	b	c	a	c	b	a	b
模式串 pattern	a	b	c

第二趟：

主串指针 len = 6 ，模式串指针 i = 4 时，模式串的 c 和主串的 b 匹配失败。已经匹配的字符串是 abca ，查看前缀表，prefix[3] = 1 ，说明 abca 前缀和后缀有一个字符相等，所以下一趟模式串要回退到第二个字符开始重新比较，也就是回退到模式串 pattern 的下标为 1 的位置。

下标	0	1	2	3	4	5	6	7	8	9	10	11	12
主串 main	a	b	a	b	c	a	b	c	a	c	b	a	b
模式串 pattern			a	b	c	a	c

第三趟：

主串指针 len = 6 ，模式串指针 i = 0 时，模式串的 a 和主串的 b 匹配失败。查看前缀表，prefix[0] = 0 ，说明前缀和后缀没有相等的，因为当前与主串比较的就是模式串的第一个字符，所以，将主串移到下一个位置，与模式串的第一个字符比较。

下标	0	1	2	3	4	5	6	7	8	9	10	11	12
主串 main	a	b	a	b	c	a	b	c	a	c	b	a	b
模式串 pattern						a	b	c	a	c

模式串全部比较完成，匹配成功。整个匹配过程中，主串始终没有回退，所以，KMP算法的时间复杂的是 O（n+m） 。

某趟发生匹配失败时，如果对应部分的前缀表是0，也就是说已匹配的相等序列中没有相等的前后缀，此时模式串移到第一个字符开始比较。

这个前缀表，似乎和写代码时用的next数组没有关系诶。

2、next数组

以 abcac 为例：

前缀表 prefix = [0,0,0,1,0] ，

用求next数组的方法求出来的数组是 next = [0,1,1,1,2] ，

这样看起来，prefix 和 next 的关系，好像并不明显，这么隐晦的吗？

next数组还有一种表达方式 next = [-1,0,0,0,1] ，这样看来来，prefix 和 next 好像有点关系了。

将前缀表整体右移一位，然后将空出来的第一位用 -1 填充，就得到了next 数组：

下标	0	1	2	3	4
字符串	a	b	c	a	c
前缀表 prefix	0	0	0	1	0
next	-1	0	0	0	1

这样，当模式串和主串匹配失败时，直接查看当前匹配失败的字符的前缀表就可以了，而不是查看匹配失败字符前一个字符的前缀表了。

next数组计算规则:

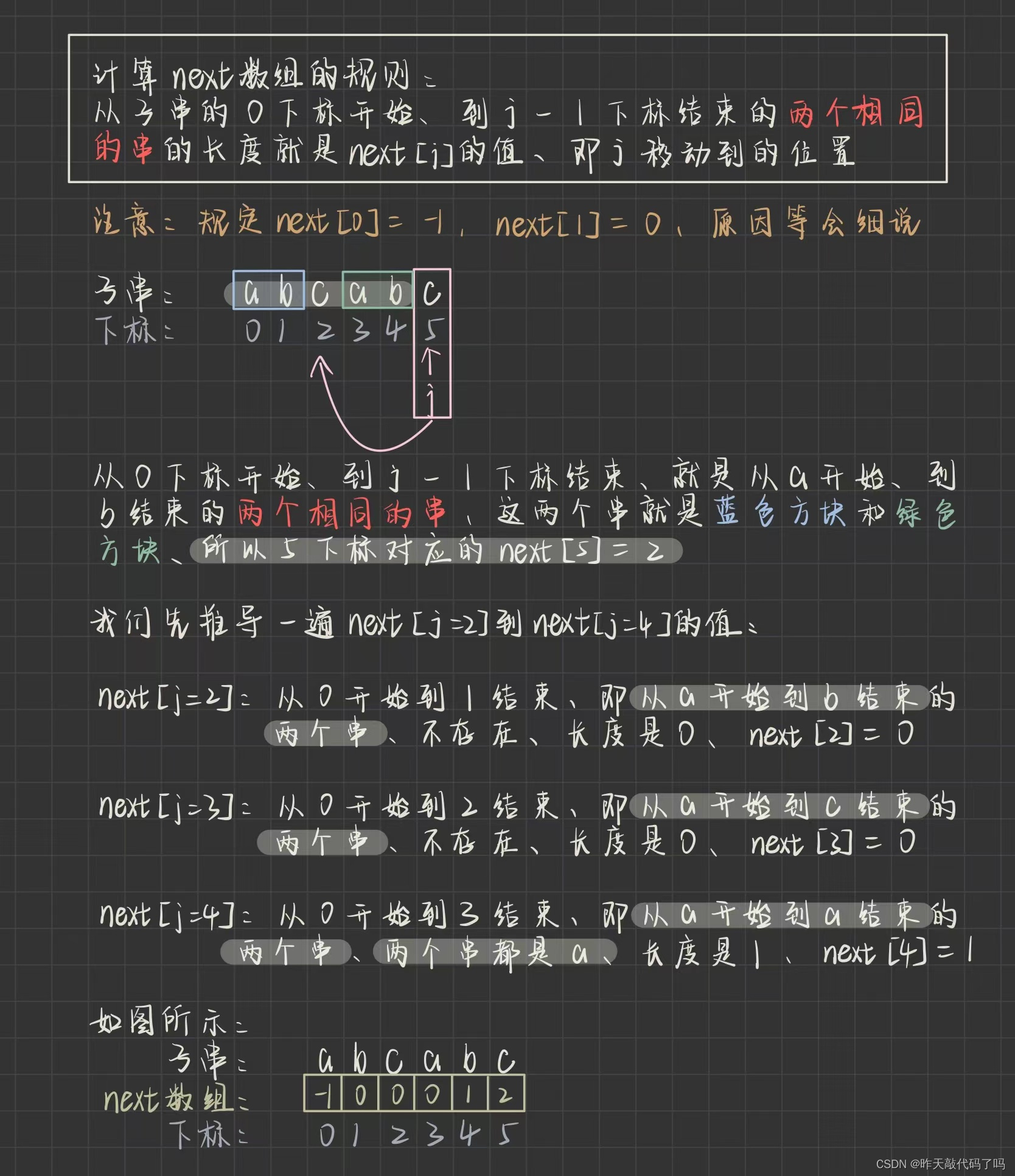
代码里应该是先定义一个 next 数组 (和子串长度相等) ，然后写一个 getNext 方法得到 next 数组中的值，那么 getNext 方法的代码如何写呢, 马上来啦！

定义变量K

注意：k 的值就是我们所说的, 子串匹配失败后 j 移动（回退）到的位置 , 继续往下看

期望情况 : charAt( j-1 ) == charAt( k )✅

非期望情况 : charAt( j-1 ) != charAt( k )❎

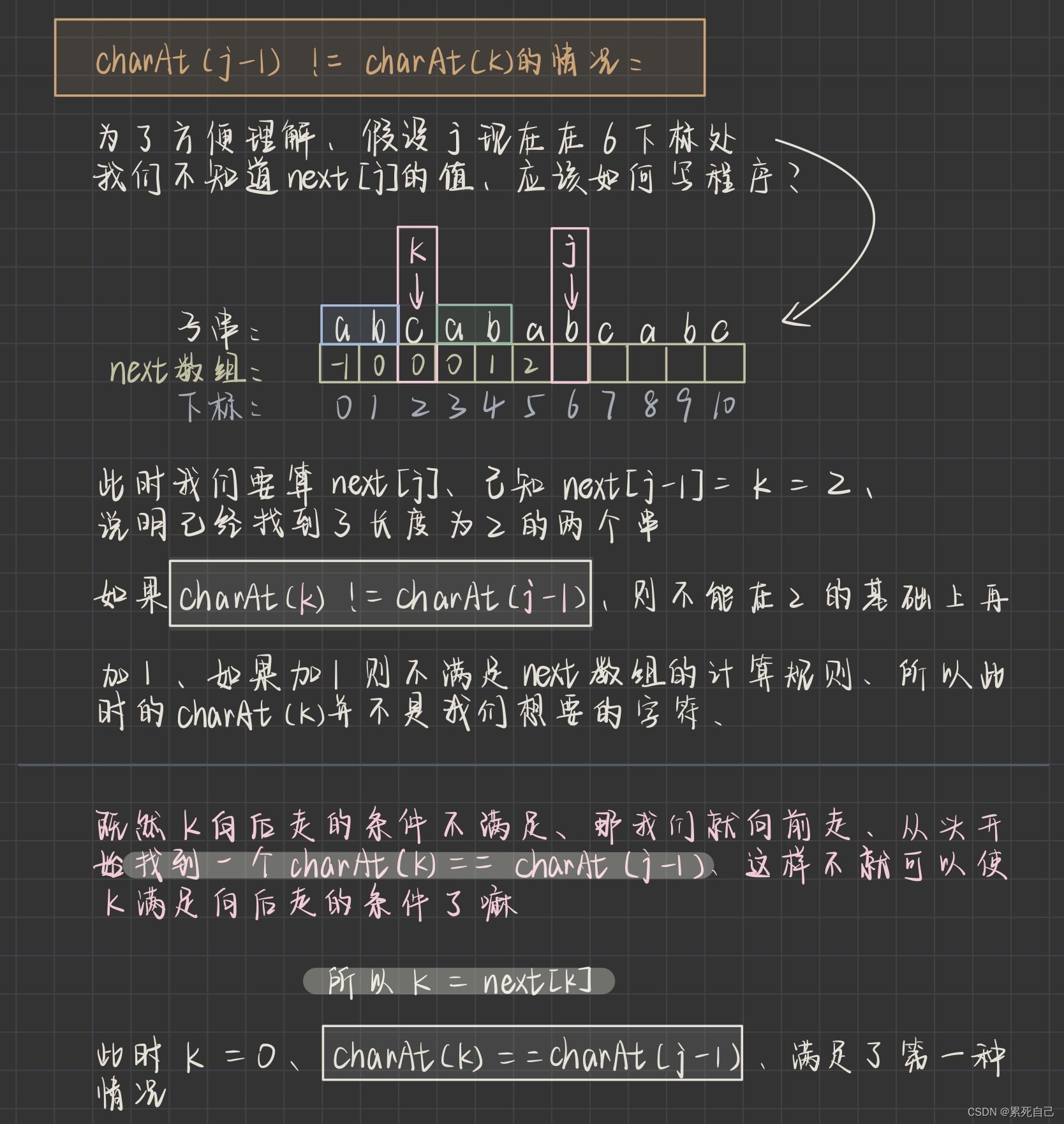
通过这两种情况的情况的对比分析可知

第 1 种情况才是理想的, 我们希望发生的
如果发生第 2 种情况, 我们就想办法改变现状, 变成第 1 种情况, 就是让 k 一直回退, 每次回退之后就判断是否满足第 1 种情况, 直到满足第 1 种情况的条件为止

public static void getNext(int[] next, String sub) {
    next[0] = -1;
    if(sub.length() == 1) {
    // 当子串只有一个数据的时候，next数组的长度为1
    	return;
    }
    // 前提条件是数组长度大于1
    next[1] = 0;
    int k = 0;
    int j = 2;

    while(j < sub.length()) {
        if(k == -1 || sub.charAt(j - 1) == sub.charAt(k)) {
            next[j] = k + 1;
            j++;
            k++;
        }else {
            k = next[k];
        }
    }
}

3、代码实现

public static int KMP(String str, String sub, int pos) {
    // 判断两个串不能为空
    if(str == null || sub == null) {
         return -1;
    }

    int i = pos;// i遍历主串  从pos位置开始
    int j = 0;  // j遍历字串  从0开始
    int strLength = str.length();
    int subLength = sub.length();
        
    if(strLength == 0 || subLength == 0) {
        return -1;
    }
    // 判断pos位置合法性
    if(pos < 0 || pos > strLength) {
        return -1;
    }

    //求字串的next数组
    int[] next = new int[subLength];
    getNext(next, sub);

    while(i < strLength && j < subLength) {
        if(j == -1 || str.charAt(i) ==  sub.charAt(j)) {
            i++;
            j++;
        }else {
            j = next[j];
        }

    }if(j == subLength) {
        // 字串遍历完之后 j应该等于sublength
        // 找到返回字串在主串中的起始位置
        return i - j;
    }else {
        // 找不到返回-1
		return -1;
	}

}

二、BM算法

BM 算法是一种高效的字符串匹配算法，名称由两个发明者姓名的首字母组成。该算法有两类规则：坏字符规则和好后缀规则，其中好后缀规则可以独立于坏字符规则使用，在内存要求比较严格时，可以只使用好后缀规则来实现。BM 算法的时间复杂度分析非常复杂，有数据表明，在实践中 BM 算法比 KMP 算法快 3-5 倍，且通常模式串越长，算法速度越快。

1、坏字符

首先，主串和模式串头部对齐，从尾部开始比较。上图中 S 和 E 不匹配，我们就称 S 为坏字符，即不匹配的字符。此时 S 也不包含在模式串中，因此可以直接移动到 S 的后一位。如下图所示：

依然从尾部开始比较，发现 P 与 E 不匹配，所以 P 是坏字符。但是 P 包含在模式串中，所以只能将模式串后移 2 位，两个 P 对齐。如下图所示：

由此总结出坏字符规则：后移位数 = 坏字符在模式串中的位置 - 坏字符在模式串中的上一次出现位置。如果坏字符不包含在模式串中，则上一次出现位置为 -1。

上一次出现位置：指最右出现的位置，即从模式串的当前位置开始，从右往左查找

以 P 为例，它作为坏字符，出现在模式串的第 6 位（从0开始编号），在模式串中的上一次出现位置为 4，所以后移 6 - 4 = 2 位。再以 S 为例，它出现在模式串的第 6 位，上一次出现位置是 -1（即未出现），所以后移 6 - (-1) = 7位，刚好是模式串的长度。

依然从尾部开始比较，MPLE 与 MPLE 匹配。我们就称 MPLE、PLE、LE、E 为好后缀，即所有尾部匹配的字符串。继续比较前一位，发现 I 与 A 不匹配，所以 I 是坏字符，按照坏字符规则，应该将模式串后移 2 - (-1) = 3 位。但是，我们这里采用好后缀规则：后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串中上一次出现的位置。如果好后缀在模式串中只出现一次，则上一次出现位置为 -1。

上一次出现位置：指最左出现的位置，即从模式串的头部开始，从左往右查找

BM 算法的基本思想是，每次后移这两个规则之中的较大值。更巧妙的是，这两个规则的移动位数，只与模式串有关，与主串无关。因此，可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时，只要查表比较一下就可以了。

此时，所有的好后缀之中，只有 E 还出现在 EXAMPLE 的头部，所以后移 6 - 0 = 6 (6 > 3) 位。如下图所示：

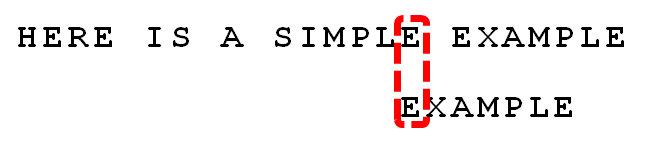
可以看到，"坏字符规则"只能移3位，"好后缀规则"可以移6位。所以，Boyer-Moore算法的基本思想是，每次后移这两个规则之中的较大值。

这个规则有三个注意点：

"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀，则它的位置以"F"为准，即5（从0开始计算）。
如果"好后缀"在搜索词中只出现一次，则它的上一次出现位置为 -1。比如，"EF"在"ABCDEF"之中只出现一次，则它的上一次出现位置为-1（即未出现）。
如果"好后缀"有多个，则除了最长的那个"好后缀"，其他"好后缀"的上一次出现位置必须在头部。比如，假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B"，请问这时"好后缀"的上一次出现位置是什么？回答是，此时采用的好后缀是"B"，它的上一次出现位置是头部，即第0位。这个规则也可以这样表达：如果最长的那个"好后缀"只出现一次，则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB"，即虚拟加入最前面的"DA"。

回到上文的这个例子。此时，所有的"好后缀"（MPLE、PLE、LE、E）之中，只有"E"在"EXAMPLE"还出现在头部，所以后移 6 - 0 = 6位。

3、代码实现

public class BM {
    // BM算法匹配字符串，匹配成功返回P在S中的首字符下标，匹配失败返回-1
    public static int indexOf(String source, String pattern) {
        char[] src = source.toCharArray();
        char[] ptn = pattern.toCharArray();
        int sLen = src.length;
        int pLen = ptn.length;

        // 模式串为空字符串，返回0
        if (pLen == 0) {
            return 0;
        }
        // 主串长度小于模式串长度，返回-1
        if (sLen < pLen) {
            return -1;
        }

        int[] BC = buildBadCharacter(ptn);
        int[] GS = buildGoodSuffix(ptn);

        // 从尾部开始匹配，其中i指向主串，j指向模式串
        for (int i = pLen - 1; i < sLen; ) {
            int j = pLen - 1;
            for (; src[i] == ptn[j]; i--, j--) {
                if (j == 0) {   // 匹配成功返回首字符下标
                    return i;
                }
            }

            // 每次后移“坏字符规则”和“好后缀规则”两者的较大值
            // 注意此时i（坏字符）已经向前移动，所以并非真正意义上的规则
            i += Math.max(BC[src[i]], GS[pLen - 1 - j]);
        }

        return -1;
    }

    // 坏字符规则表
    private static int[] buildBadCharacter(char[] pattern) {
        int pLen = pattern.length;
        final int CHARACTER_SIZE = 256; // 英文字符的种类，2^8
        int[] BC = new int[CHARACTER_SIZE]; // 记录坏字符出现时后移位数

        Arrays.fill(BC, pLen);  // 默认后移整个模式串长度
        for (int i = 0; i < pLen - 1; i++) {
            int ascii = pattern[i];  // 当前字符对应的ASCII值
            BC[ascii] = pLen - 1 - i;   // 对应的后移位数，若重复则以最右边为准
        }

        return BC;
    }

    // 非真正意义上的好字符规则表，后移位数还加上了当前好后缀的最大长度
    private static int[] buildGoodSuffix(char[] pattern) {
        int pLen = pattern.length;
        int[] GS = new int[pLen];   // 记录好后缀出现时后移位数
        int lastPrefixPos = pLen;   // 好后缀的首字符位置

        for (int i = pLen - 1; i >= 0; i--) {
            // 判断当前位置（不含）之后是否是好后缀，空字符也是好后缀
            if (isPrefix(pattern, i + 1)) {
                lastPrefixPos = i + 1;
            }
            // 如果是好后缀，则GS=pLen，否则依次为pLen+1、pLen+2、...
            GS[pLen - 1 - i] = lastPrefixPos - i + pLen - 1;
        }

        // 上面在比较好后缀时，是从模式串的首字符开始的，但实际上好后缀可能出现在模式串中间。
        // 比如模式串EXAMPXA，假设主串指针在比较P时发现是坏字符，那么XA就是好后缀，
        // 虽然它的首字符X与模式串的首字符E并不相等。此时suffixLen=2表示将主串指针后移至模式串末尾，
        // pLen-1-i=4表示真正的好字符规则，同样主串指针后移，使得模式串前面的XA对齐主串的XA
        for (int i = 0; i < pLen - 1; i++) {
            int suffixLen = suffixLength(pattern, i);
            GS[suffixLen] = pLen - 1 - i + suffixLen;
        }

        return GS;
    }

    // 判断是否是好后缀，即模式串begin（含）之后的子串是否匹配模式串的前缀
    private static boolean isPrefix(char[] pattern, int begin) {
        for (int i = begin, j = 0; i < pattern.length; i++, j++) {
            if (pattern[i] != pattern[j]) {
                return false;
            }
        }

        return true;
    }

    // 返回模式串中以pattern[begin]（含）结尾的后缀子串的最大长度
    private static int suffixLength(char[] pattern, int begin) {
        int suffixLen = 0;

        int i = begin;
        int j = pattern.length - 1;
        while (i >= 0 && pattern[i] == pattern[j]) {
            suffixLen++;
            i--;
            j--;
        }

        return suffixLen;
    }
}