DLX舞蹈链

一、精确覆盖问题

精确覆盖问题（英文：Exact Cover Problem）是指给定许多集合 $S_i(1\le i\le n)$ 以及一个集合 $X$，求满足以下条件的无序多元组 $(T_1,T_2,\cdots ,T_m)$：

1. $\mathrm{\forall }i,j\in [1,m],T_i\bigcap T_j=\varnothing (i\ne j)$
2. $X=\bigcup _{i=1}^m{T}_i$
3. $\mathrm{\forall }i\in [1,m],T_i\in \{S_1,S_2,\cdots ,S_n\}$

例如，若给出

$$\begin{array}{rl}& S_1=\{5,9,17\}\\ & S_2=\{1,8,119\}\\ & S_3=\{3,5,17\}\\ & S_4=\{1,8\}\\ & S_5=\{3,119\}\\ & S_6=\{8,9,119\}\\ & X=\{1,3,5,8,9,17,119\}\end{array}$$

则 $(S_1,S_4,S_5)$ 为一组合法解。

问题转化

将 $\bigcup _{i=1}^n{S}_i$ 中的所有数离散化，可以得到这么一个模型：

给定一个 01 矩阵，你可以选择一些行（row），使得最终每列（column）都恰好有一个 1。 举个例子，我们对上文中的例子进行建模，可以得到这么一个矩阵：

$$\left(\begin{array}{ccccccc}0& 0& 1& 0& 1& 1& 0\\ 1& 0& 0& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)$$

其中第 $i$ 行表示着 $S_i$，而这一行的每个数依次表示 $[1\in S_i],[3\in S_i],[5\in S_i],\cdots ,[119\in S_i]$。

过程

继续以上文中中提到的例子为载体，得到一个这样的 01 矩阵：

$$\left(\begin{array}{ccccccc}0& 0& 1& 0& 1& 1& 0\\ 1& 0& 0& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)$$

1. 此时第一行有 $3$ 个 $1$，第二行有 $3$ 个 $1$，第三行有 $3$ 个 $1$，第四行有 $2$ 个 $1$，第五行有 $2$ 个 $1$，第六行有 $3$ 个 $1$。选择第一行，将它删除，并将所有 $1$ 所在的列打上标记；

   $$\left(\begin{array}{ccccccc}0& 0& 1& 0& 1& 1& 0\\ 1& 0& 0& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)$$

2. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记（重复覆盖问题无需打标记）；

   $$\left(\begin{array}{ccccccc}0& 0& 1& 0& 1& 1& 0\\ 1& 0& 0& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)$$

3. 选择所有被标记的行，将它们删除；

   $$\left(\begin{array}{ccccccc}0& 0& 1& 0& 1& 1& 0\\ 1& 0& 0& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)$$

   这表示这一行已被选择，且这一行的所有 $1$ 所在的列不能有其他 $1$ 了。

   于是得到一个新的小 01 矩阵：

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

4. 此时第一行（原来的第二行）有 $3$ 个 $1$，第二行（原来的第四行）有 $2$ 个 $1$，第三行（原来的第五行）有 $2$ 个 $1$。选择第一行（原来的第二行），将它删除，并将所有 $1$ 所在的列打上标记；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

5. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

6. 选择所有被标记的行，将它们删除；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

   这样就得到了一个空矩阵。但是上次删除的行 1 0 1 1 不是全 $1$ 的，说明选择有误；

   $$\left(\begin{array}{}\end{array}\right)$$

7. 回溯到步骤 4，考虑选择第二行（原来的第四行），将它删除，并将所有 $1$ 所在的列打上标记；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

8. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

9. 选择所有被标记的行，将它们删除；

   $$\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)$$

   于是我们得到了这样的一个矩阵：

   $$\left(\begin{array}{cc}1& 1\end{array}\right)$$

10. 此时第一行（原来的第五行）有 $2$ 个 $1$，将它们全部删除，得到一个空矩阵：

    $$\left(\begin{array}{}\end{array}\right)$$

11. 上一次删除的时候，删除的是全 $1$ 的行，因此成功，算法结束。

    答案即为被删除的三行：$1,4,5$。

强烈建议自己模拟一遍矩阵删除、还原与回溯的过程后，再接着阅读下文。

从上面的求解过程来看，实际上求解过程可以如下表示

1、从矩阵中选择一行

2、根据定义，标示矩阵中其他行的元素

3、删除相关行和列的元素，得到新矩阵

4、如果新矩阵是空矩阵，并且之前的一行都是1，那么求解结束，跳转到6；新矩阵不是空矩阵，继续求解，跳转到1；新矩阵是空矩阵，之前的一行中有0，跳转到5

5、说明之前的选择有误，回溯到之前的一个矩阵，跳转到1；如果没有矩阵可以回溯，说明该问题无解，跳转到7

6、求解结束，把结果输出

7、求解结束，输出无解消息

从如上的求解流程来看，在求解的过程中有大量的缓存矩阵和回溯矩阵的过程。而如何缓存矩阵以及相关的数据（保证后面的回溯能正确恢复数据），也是一个比较头疼的问题（并不是无法解决）。以及在输出结果的时候，如何输出正确的结果（把每一步的选择转换为初始矩阵相应的行）。

于是算法大师Donald E.Knuth（《计算机程序设计艺术》的作者）出面解决了这个方面的难题。他提出了DLX（Dancing Links X）算法。实际上，他把上面求解的过程称为X算法，而他提出的舞蹈链（Dancing Links）实际上并不是一种算法，而是一种数据结构。一种非常巧妙的数据结构，他的数据结构在缓存和回溯的过程中效率惊人，不需要额外的空间，以及近乎线性的时间。而在整个求解过程中，指针在数据之间跳跃着，就像精巧设计的舞蹈一样，故Donald E.Knuth把它称为Dancing Links（中文译名舞蹈链）。

二、舞蹈链

Dancing Links用的数据结构是交叉十字循环双向链,核心是基于双向链的方便操作（移除、恢复加入）

下图就是根据题目构建好的交叉十字循环双向链

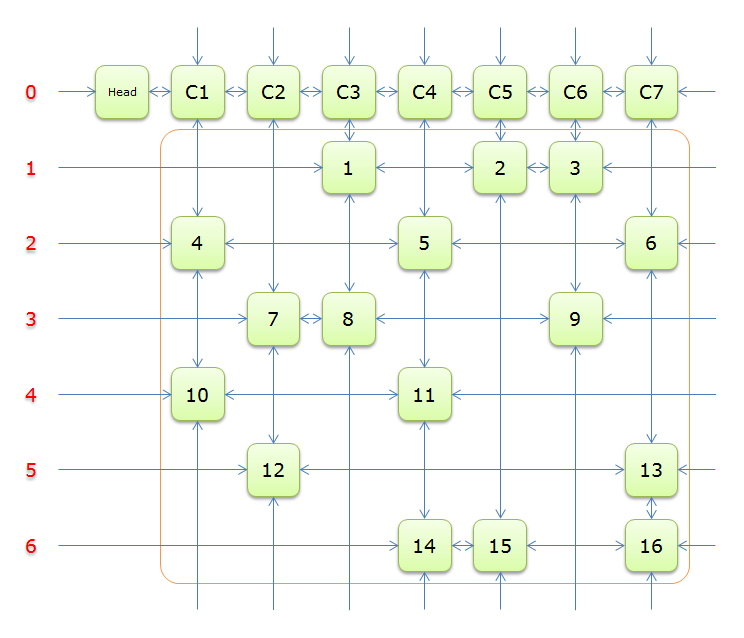
整体链表的最上端是哨兵节点 。

对于每一个节点而言：

• 首先，对于每一个节点而言，他的四个方向都被链接，所以称为十字链表。
• 其次，每一条链接都是双向的，可以由左节点访问右节点，也可以有右节点访问左节点，所以它又是双向链表。
• 最后，它的行和列都是循环的，意味着可以通过每一列的哨兵节点向上访问列的最末节点。每一行也是同样的，具有循环链表的性质。

接下来，利用图来解释Dancing Links是如何求解精确覆盖问题。

1. 首先判断Head.Right=Head？若是，求解结束，输出解；若不是，求解还没结束，到步骤2（也可以判断Head.Left=Head？）

2. 获取Head.Right元素，即元素C1，并标示元素C1（标示元素C1，指的是标示C1、和C1所在列的所有元素、以及该元素所在行的元素，并从双向链中移除这些元素）。如下图中的紫色部分。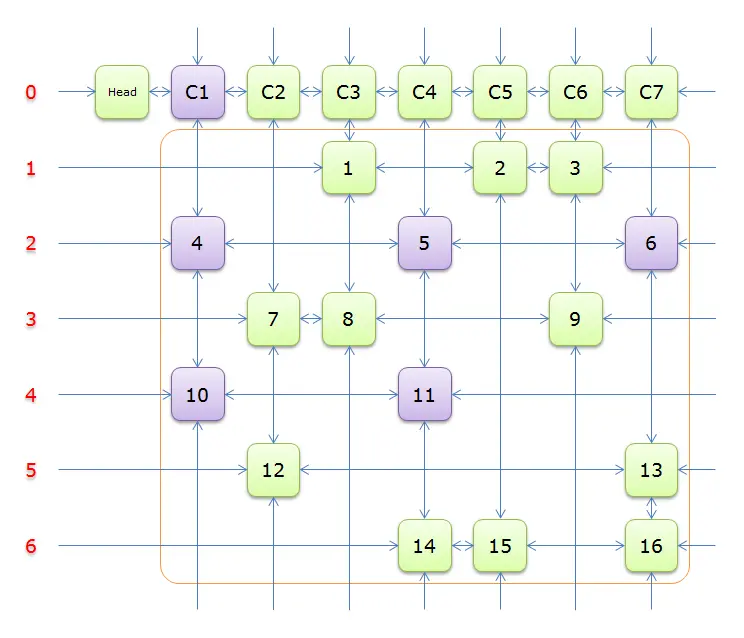

   

   如上图可知，行2和行4中的一个必是答案的一部分（其他行中没有元素能覆盖列C1），先假设选择的是行2.

3. 选择行2（在答案栈中压入2），标示该行中的其他元素（元素5和元素6）所在的列首元素，即标示元素C4和标示元素C7，下图中的橙色部分。 注意的是，即使元素5在步骤2中就从双向链中移除，但是元素5的Col分量还是指向元素C4的，这里体现了双向链的强大作用。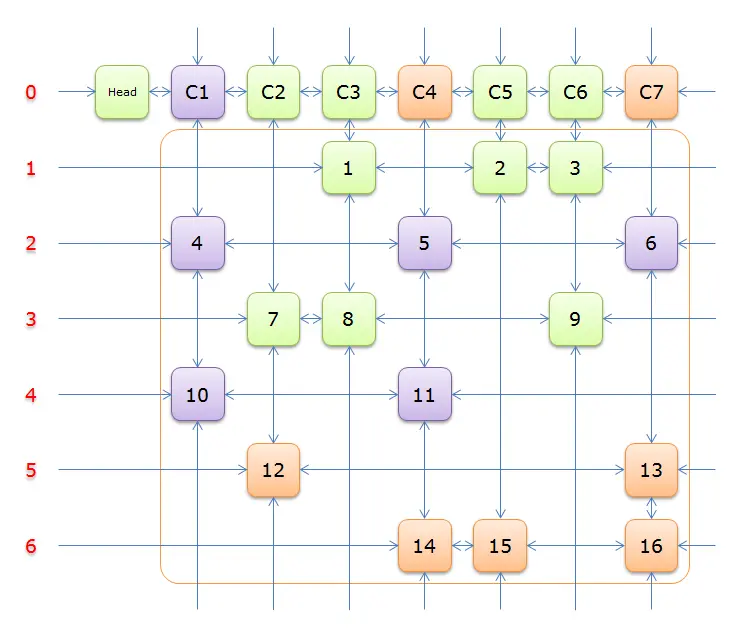

   

   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

   

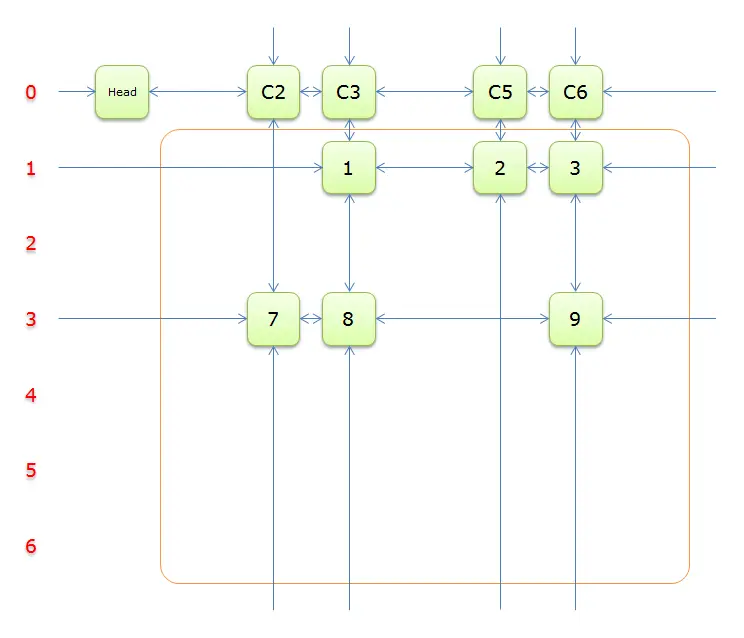
   一下子空了好多，是不是转换为一个少了很多元素的精确覆盖问题？，利用递归的思想，很快就能写出求解的过程来。我们继续完成求解过程

4. 获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。

   

   如图，列C2只有元素7覆盖，故答案只能选择行3.

5. 选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。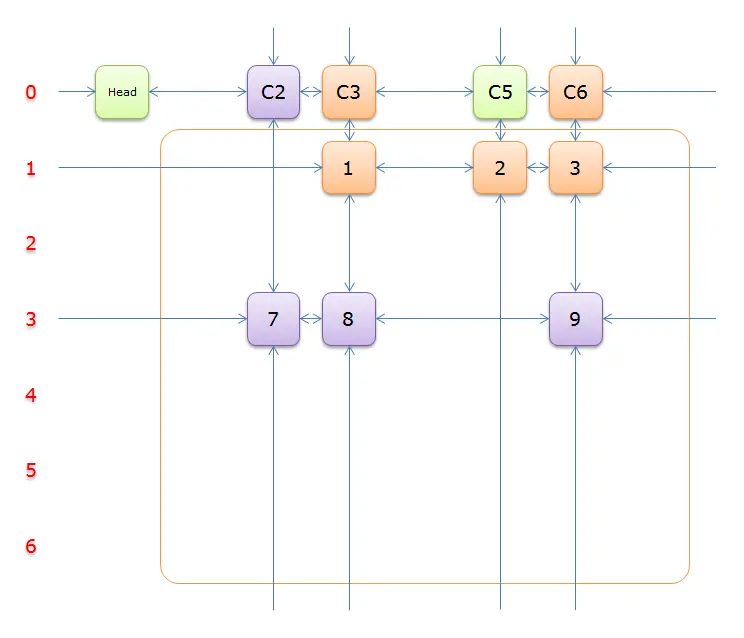

   

   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

   

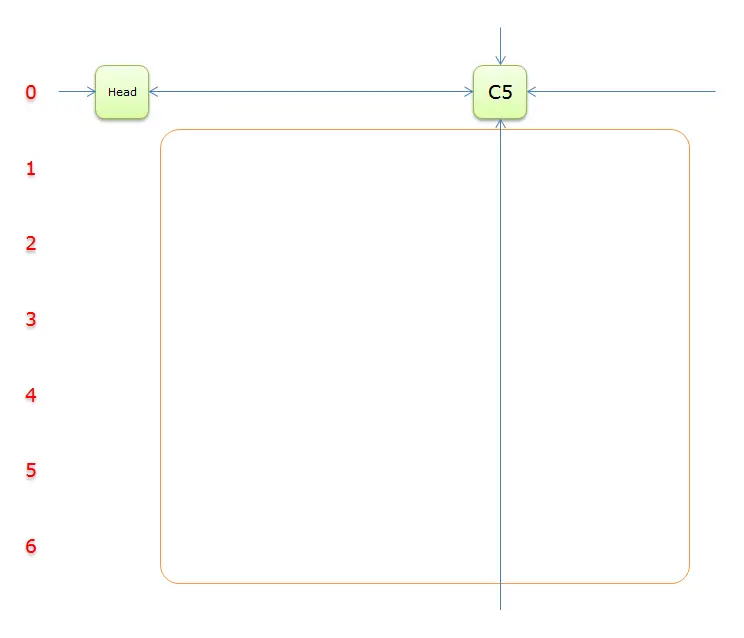
6. 获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤2）。那要回标列首元素（把列首元素、所在列的元素，以及对应行其余的元素。并恢复这些元素到双向链中），回标列首元素的顺序是标示元素的顺序的反过来。从前文可知，顺序是回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4。表面上看起来比较复杂，实际上利用递归，是一件很简单的事。并把答案栈恢复到步骤2（清空的状态）的时候。又回到下图所示:

   

7. 由于之前选择行2导致无解，因此这次选择行4（再无解就整个问题就无解了）。选择行4（在答案栈中压入4），标示该行中的其他元素（元素11）所在的列首元素，即标示元素C4，下图中的橙色部分。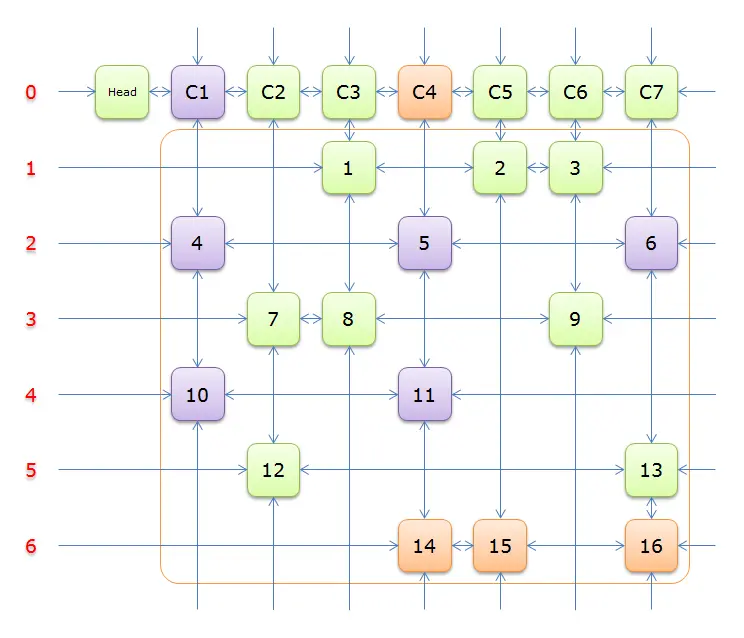

   

   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

   

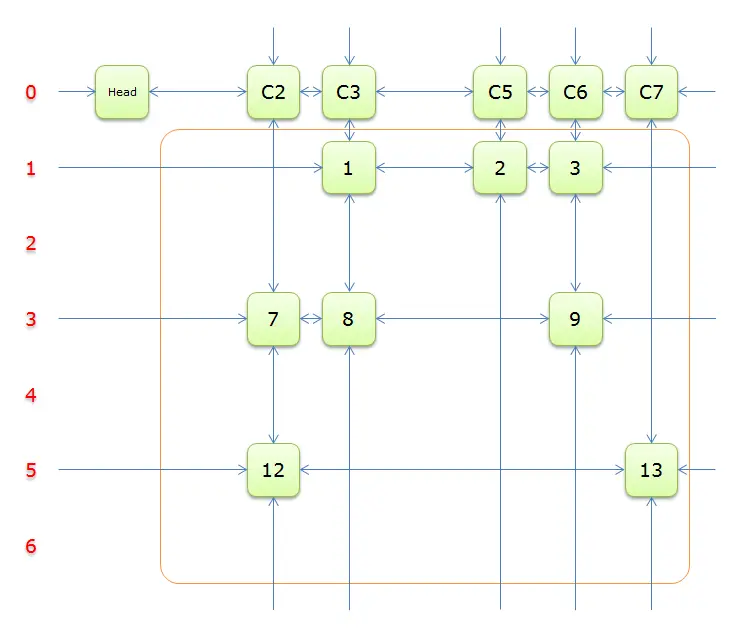
8. 获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。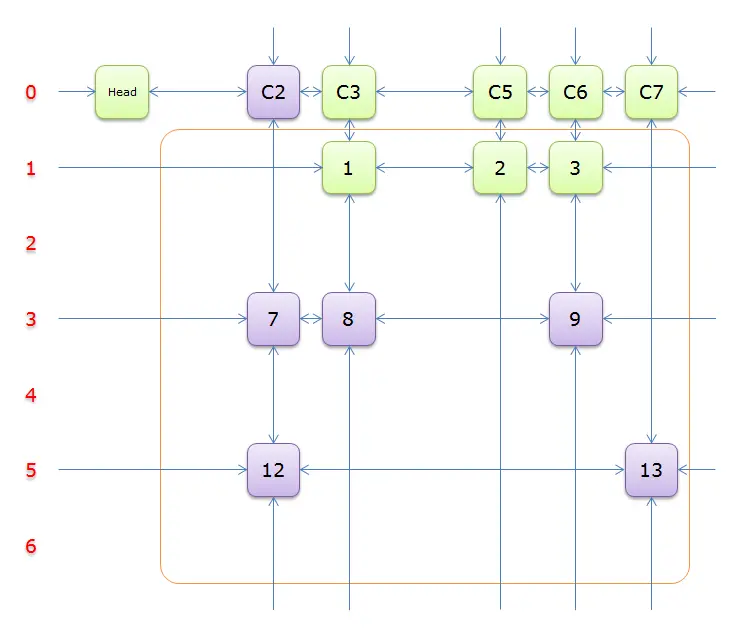

   

   如图，行3和行5都可以选择

9. 选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。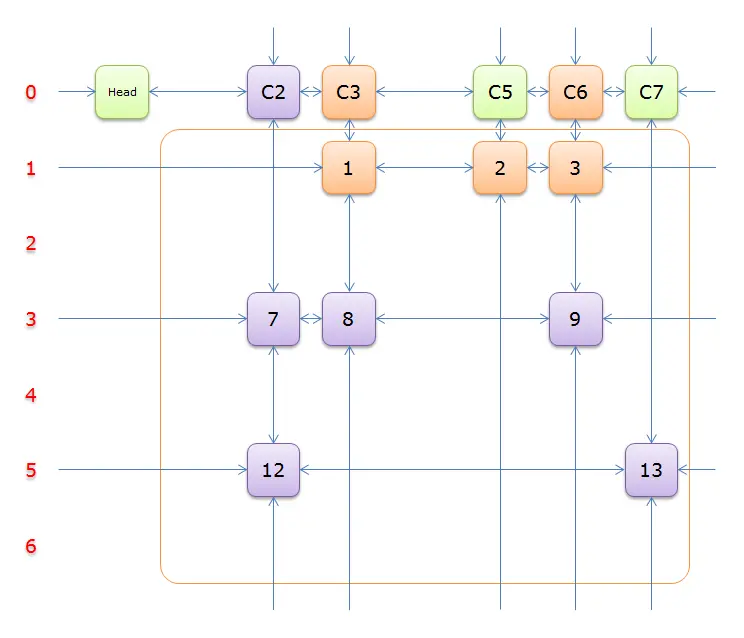

   

   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

   

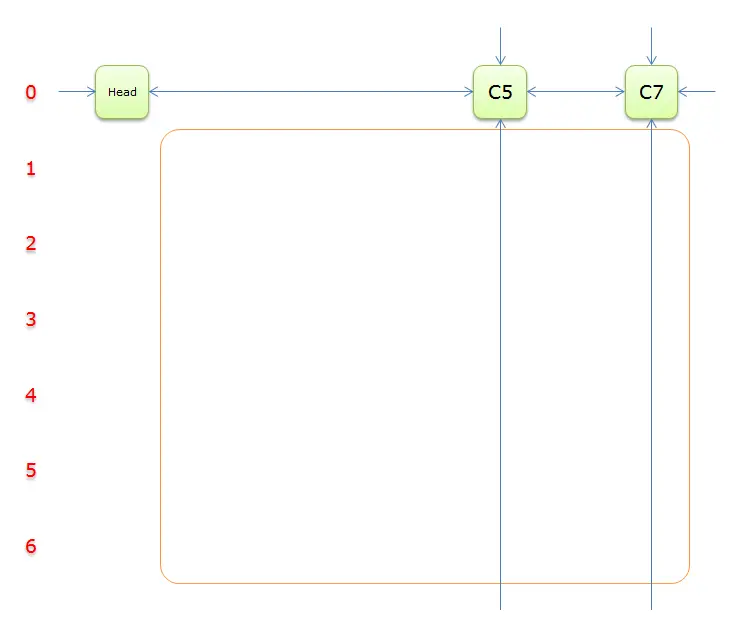
10. 获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤8）。从前文可知，回标列首C6、回标列首C3。并把答案栈恢复到步骤8（答案栈中只有4）的时候。又回到下图所示:

    

11. 由于之前选择行3导致无解，因此这次选择行5（在答案栈中压入5），标示该行中的其他元素（元素13）所在的列首元素，即标示元素C7，下图中的橙色部分。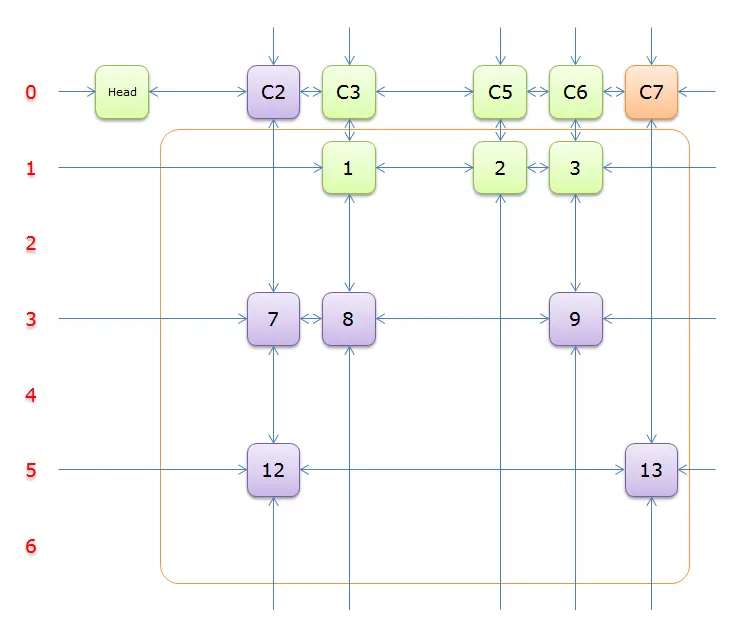

    

    把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

    

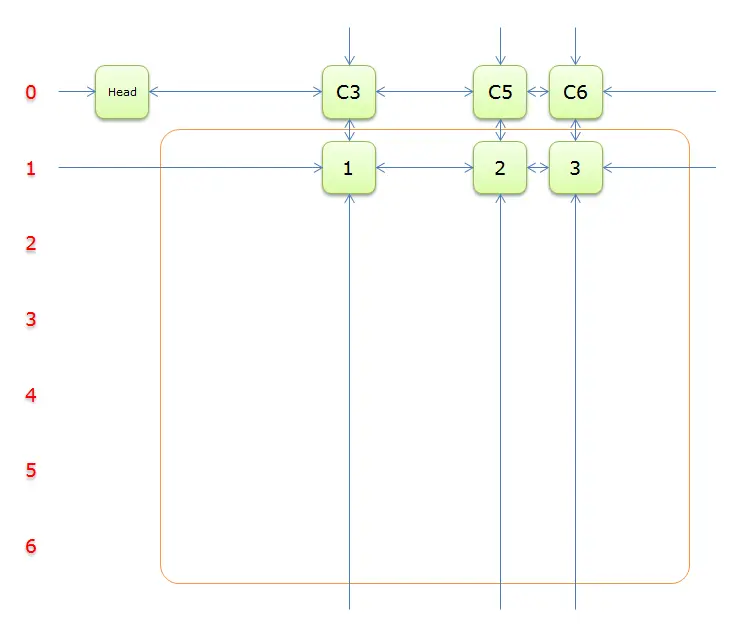
    获取Head.Right元素，即元素C3，并标示元素C3。如下图中的紫色部分。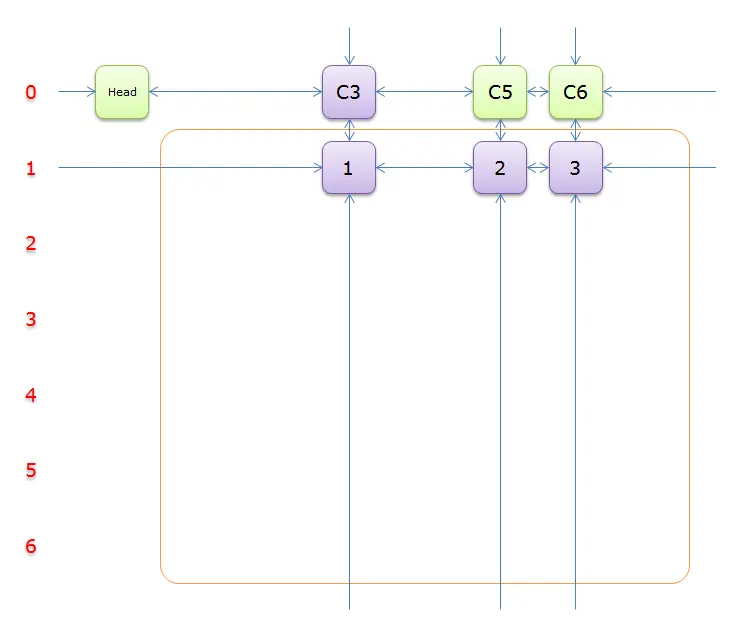

    

12. 如上图，列C3只有元素1覆盖，故答案只能选择行3（在答案栈压入1）。标示该行中的其他元素（元素2和元素3）所在的列首元素，即标示元素C5和标示元素C6，下图中的橙色部分。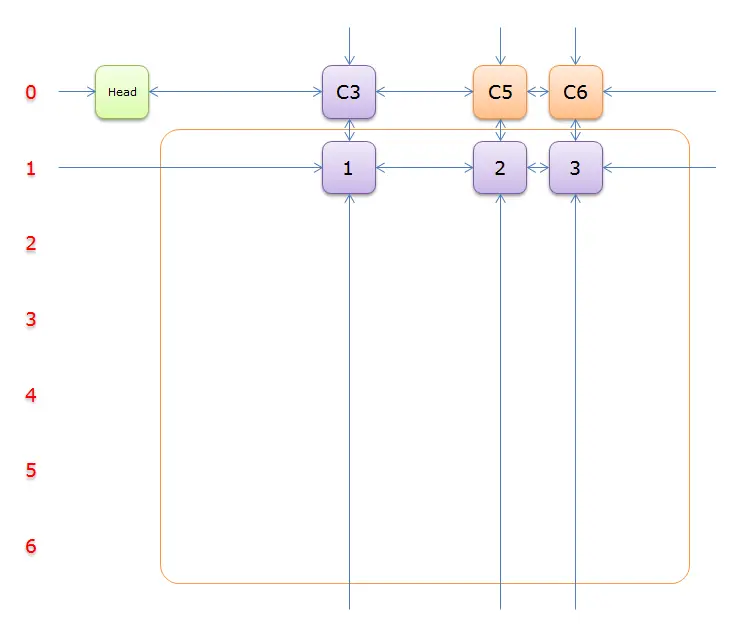

    

    把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:

    

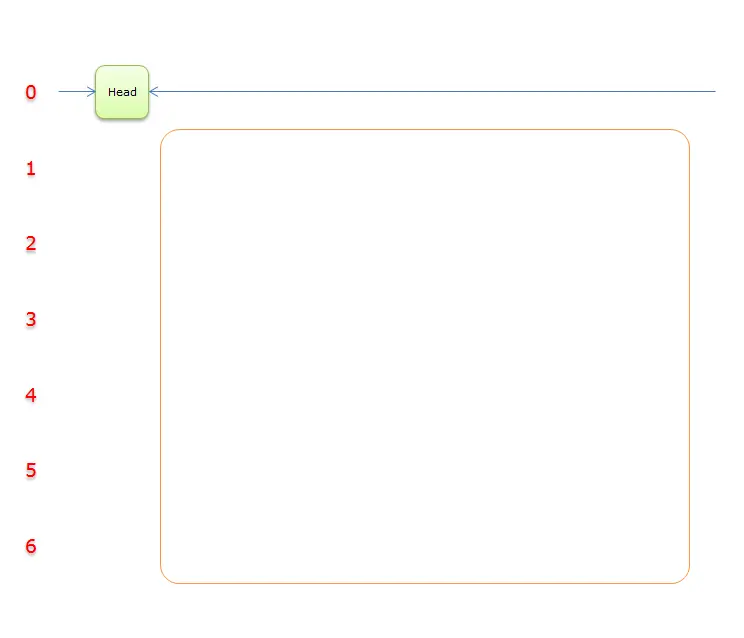
13. 因为Head.Right=Head。故，整个过程求解结束。输出答案，答案栈中的答案分别是4、5、1。表示该问题的解是第4、5、1行覆盖所有的列。如下图所示（蓝色的部分）: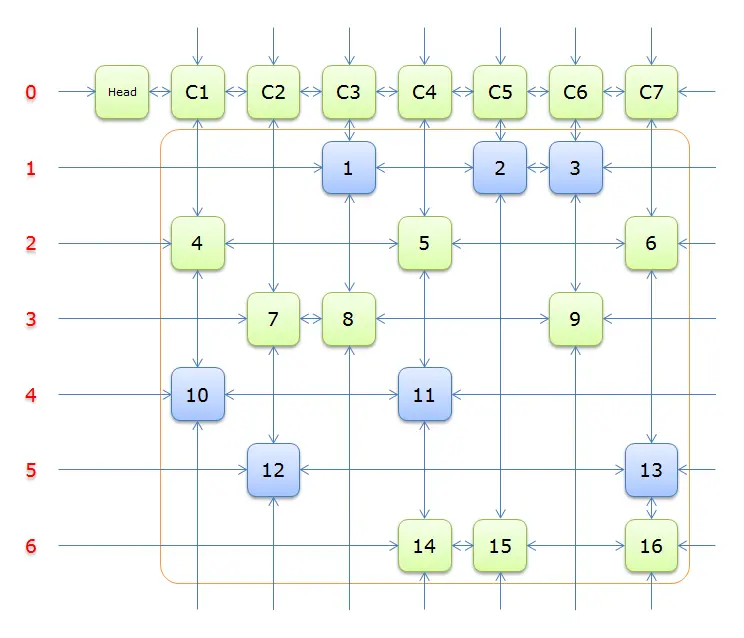

    

Dancing Links的求解过程表述如下

1、Dancing函数的入口

2、判断Head.Right=Head？，若是，输出答案，返回True，退出函数。

3、获得Head.Right的元素C

4、标示元素C

5、获得元素C所在列的一个元素

6、标示该元素同行的其余元素所在的列首元素

7、获得一个简化的问题，递归调用Daning函数，若返回的True，则返回True，退出函数。

8、若返回的是False，则回标该元素同行的其余元素所在的列首元素，回标的顺序和之前标示的顺序相反

9、获得元素C所在列的下一个元素，若有，跳转到步骤6

10、若没有，回标元素C，返回False，退出函数。

三、代码

1、舞蹈链

我们使用数组的形式来表示舞蹈链，以解决数独问题为例(leetcode-37)，代码如下

public class DLX {
    //行数，列数，总节点数
    int rowNums, columnNums, totalNums;
    // left[i]：第i个节点的左节点
    int[] left, right, up, down, rowIndexs, colIndexs;
    //记录第i行的头指针
    int [] headers;
    //记录结果
    int [] res;
    int resNum; //结果数量
    //统计每一列的节点数量
    int[] columnCount;

    public DLX(int n){
        int maxRowNum = n*n*n + 10;
        int maxColumnNum = n*n*4 + 10;
        int maxNodeNum = maxRowNum * 4 + maxColumnNum;
        left = new int[maxNodeNum];
        right = new int[maxNodeNum];
        up = new int[maxNodeNum];
        down = new int[maxNodeNum];
        rowIndexs = new int[maxNodeNum];
        colIndexs = new int[maxNodeNum];
        headers = new int[maxRowNum];
        columnCount = new int[maxColumnNum];
        res = new int[maxRowNum];
    }

    public void init(int rowNums, int columnNums){
        this.rowNums = rowNums;
        this.columnNums = columnNums;
        //初始化第一行，表头
        for(int i=0; i<=columnNums;i++){
            columnCount[i] = 0;
            left[i] = i-1;
            right[i] = i+1;
            up[i] = down[i] = i;
        }
        left[0] = columnNums;
        right[columnNums] = 0;
        totalNums = columnNums;
        //初始化每一行的头指针
        for(int i=1; i<=rowNums;i++){
            headers[i] = -1;
        }
    }

    //插入点（rowIndex, columnIndex)第rowindex行，第columnIndex列
    public void addNode(int rowIndex, int columnIndex){
        columnCount[colIndexs[++totalNums] = columnIndex]++;
        rowIndexs[totalNums] = rowIndex;

        up[totalNums] = columnIndex; down[totalNums] = down[columnIndex];
        up[down[columnIndex]] = totalNums; down[columnIndex] = totalNums;

        if(headers[rowIndex] == -1){
            headers[rowIndex] = left[totalNums] = right[totalNums] = totalNums;
        }else{
            left[totalNums] = headers[rowIndex]; right[totalNums] = right[headers[rowIndex]];
            left[right[headers[rowIndex]]] = totalNums; right[headers[rowIndex]] = totalNums;
        }
    }

    //删除啊一列，将该列为1的行都删除
    public void removeColumn(int columnIndex){
        left[right[columnIndex]] = left[columnIndex];
        right[left[columnIndex]] = right[columnIndex];
        for(int i=down[columnIndex]; i!= columnIndex;i=down[i]){
            for(int j=right[i]; j!= i; j=right[j]){
                up[down[j]] = up[j];
                down[up[j]] = down[j];
                columnCount[colIndexs[j]]--;
            }
        }
    }

  //恢复一列，将该列为1的行恢复
    public void resumeColumn(int columnIndex){
        for(int i=up[columnIndex];i!=columnIndex;i=up[i]){
            for(int j=left[i]; j!= i;j=left[j]){
                up[down[j]] = j;
                down[up[j]] = j;
                columnCount[colIndexs[j]]++;
            }
        }
        left[right[columnIndex]] = columnIndex;
        right[left[columnIndex]] = columnIndex;
    }

    /**
     *
     * @param d 选取了d行
     */
    public boolean dance(int d){
        if(right[0] == 0){
            resNum = d;
            return true;
        }
        int removeCol = right[0];
        for(int i=removeCol; i!=0; i=right[i]){
            if(columnCount[i] < columnCount[removeCol])
                removeCol = i;
        }
        removeColumn(removeCol);
        for(int i=down[removeCol]; i!=removeCol; i=down[i]){
            res[d] = rowIndexs[i];
            for(int j=right[i]; j!=i; j=right[j]) removeColumn(colIndexs[j]);
            if(dance(d+1)) return true;
            for(int j=right[i]; j!=i; j=right[j]) resumeColumn(colIndexs[j]);
        }
        resumeColumn(removeCol);
        return false;
    }

}

2、数独

矩阵的列

将数独问题转换成精确覆盖问题我们把矩阵的每个列都定义成一个约束条件。

第1列定义成：（1，1）填了一个数字
第2列定义成：（1，2）填了一个数字
...
第9列定义成：（1，9）填了一个数字
第10列定义成：（2，1）填了一个数字
...
第18列定义成：（2，9）填了一个数字
...
第81列定义成：（9，9）填了一个数字

至此，用第1-81列完成了约束条件1：每个格子只能填一个数字

第N列（1≤N≤81）定义成：（X，Y）填了一个数字。N、X、Y之间的关系是：X = INT((N - 1)/ 9)+1; Y = ((N-1) Mod 9) + 1; N =(X - 1) × 9 + Y.

第82列定义成：在第1行填了数字1
第83列定义成：在第1行填了数字2
...
第90列定义成：在第1行填了数字9
第91列定义成：在第2行填了数字1
...
第99列定义成：在第2行填了数字9
...
第162列定义成：在第9行填了数字9

至此，用第82-162列（共81列）完成了约束条件2：每行1-9的这9个数字都得填一遍

第N列（82≤N≤162）定义成：在第X行填了数字Y。N、X、Y之间的关系是：X = INT(N - 81 - 1)/ 9)+ 1; Y = ((N - 81 - 1)Mod 9)+ 1; N = (X - 1)× 9 + Y + 81.

第163列定义成：在第1列填了数字1
第164列定义成：在第1列填了数字2
...
第171列定义成：在第1列填了数字9
第172列定义成：在第2列填了数字1
...
第180列定义成：在第2列填了数字9
...
第243列定义成：在第9列填了数字9

至此，用第163-243列（共81列）完成了约束条件3：每列1-9的这9个数字都得填一遍

第N列（163≤N≤243）定义成：在第X列填了数字Y。N、X、Y之间的关系是：X = INT((N - 162 - 1) / 9) + 1; Y =((N - 162 - 1)Mod 9) + 1; N = (X - 1)× 9 + Y + 162.

第244列定义成：在第1宫填了数字1
第245列定义成：在第1宫填了数字2
...
第252列定义成：在第1宫填了数字9
第253列定义成：在第2宫填了数字1
...
第261列定义成：在第2宫填了数字9
...
第324列定义成：在第9宫填了数字9

至此，用第244-324列（共81列）完成了约束条件4：每宫1-9的这9个数字都得填一遍

第N列（244≤N≤324）定义成：在第X宫填了数字Y。N、X、Y之间的关系是：X = INT((N - 243 - 1) / 9)+ 1; Y = ((N - 243 - 1)Mod 9)+ 1; N = (X - 1) × 9 + Y + 243.

至此，用了324列完成了数独的四个约束条件，矩阵的列定义完成.

矩阵的行

第1-9行分别表示（1，1）位置填入1-9，依次类推，因此(i,j)处填入k在第(i*9+j)*9+k行

这样，从数独的格子依次转换成行（1行或者9行）插入到矩阵中。完成了数独问题到精确覆盖问题的转换。接下来求解精确覆盖问题就可以交给舞蹈链（Dancing Links）算法了.

public class Solution{
    //编码需要根据图的性质进行调整，这个编码只针对对于9*9数独的等价限制条件
    public int[] encode(int i,int j,int k){
        int r=(i*9+j)*9+k;
        int c1=81*0+i*9+j+1;
        int c2=81*1+i*9+k;
        int c3=81*3+j*9+k;
        int c4=81*2+((i/3)*3+(j/3))*9+k;
        return new int[]{r,c1,c2,c3,c4};
    }

    public void solveSudoku(char[][] board){
        DLX dlx=new DLX(9);
        dlx.init(9*9*9,9*9*4);
        int[]code;
        for(int i=0;i<9;i++)
            for(int j=0;j<9;j++)
                for(int k=1;k<=9;k++)
                    if(board[i][j]=='.' || board[i][j]=='0'+k){
                        code=encode(i,j,k);
                        dlx.addNode(code[0],code[1]);
                        dlx.addNode(code[0],code[2]);
                        dlx.addNode(code[0],code[3]);
                        dlx.addNode(code[0],code[4]);
                    }
        dlx.dance(0);
        int v,x,y;
        for(int i=0;i<dlx.resNum;i++){
            v=(dlx.res[i]-1)%9+1;//这里记得加回1，从'1'~'9'
            x=(dlx.res[i]-1)/9/9;//开始编码的，不是'0'~'8'
            y=(dlx.res[i]-1)/9%9;//否则下面将采用(char)('1'+v)
            board[x][y]=(char)('0'+v);
        }

    }
}

参考

[1] https://oi-wiki.org/search/dlx/

[2] https://www.cnblogs.com/grenet/p/3145800.html

[3] https://blog.csdn.net/m0_52447591/article/details/120250353